
Resolving power is an index used to represent the limit of spatial observation. In optics, the minimum detectable distance between two image points is called resolving limit, and the reverse is defined as the resolving power.
There are several methods to measure the resolving limit or resolving power. Two such methods, (1) resolving power by refraction and (2) MTF, are introduced below.
(1) Resolving limit by refraction
Theoretically an object point will be projected as a point on an image plane if the optical system has no aberration. However, because of diffraction the image of a point will be a circle with a radius of about one wavelength of light, which in called the Airy pattern, as shown in Figure 2.3.1. Therefore there exists a limit to resolve the distance between two points even though there is no aberration.
The resolving limit depends on how the minimum distance between two Airy images is defined. There are two definitions, as follows.
a. Rayleigh's resolving power: the distance between the left Airy peak and the right Airy peak when it coincides with the zero point of the left peak, that is 1.22u in Figure 2.3.2.
b. Sparrow's resolving limit: the distance between the two peaks when the central gap fades away, that is 1.08u in Figure 2.3.3 .
(2) MTF (modular transfer function )
The resolving power measured on a resolving test chart by human eyes, depends on individual ability and the shape or contrast of the chart. On the other hand, MTF has no such problems because MTF comes from a scientific definition in which the response of spatial frequency, with respect to the amplitude, considers the optical imaging system as a spatial frequency filter.
As the spatial frequency is defined as the frequency of a sine wave, MTF shows how much the ratio of the amplitude decreases before and after an optical imaging system with respect to the spatial frequency as shown in Figure 2.3.4.
MTF coincides with the power spectrum which is obtained by Fourier transformation of a point image. Generally speaking, an optical imaging system will give a low pass filter as shown in Figure 2.3.5.
Modulation (M), contrast (K) and density (D) have the following relations.
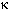 =
=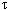 max /
max /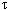 min,
D = log(
min,
D = log(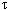 max /
max /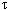 min),
M = (
min),
M = ( 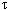 max -
max - 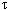 min ) / (
min ) / ( 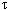 max +
max + 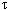 min ) =
(
min ) =
( 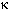 - 1) / (
- 1) / ( 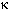 + 1)
+ 1)
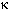 ' =
' =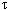 'max /
'max /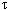 'min,
D' = log(
'min,
D' = log(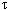 'max /
'max /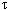 min),
M = (
min),
M = ( 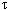 'max -
'max - 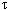 'min ) / (
'min ) / ( 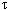 'max +
'max + 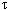 'min ) =
(
'min ) =
( 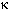 ' - 1) / (
' - 1) / ( 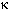 ' + 1)
' + 1)
The resolving power (or spatial frequency) is obtained from the MTF curve with a given contrast, which can be converted to the modulation.

Copyright © 1996 Japan Association of Remote Sensing All rights reserved