
| Table des matières |
| 1. Introduction 2. Capteurs 3. Hyperfréquences |
4. Analyse d'image |
| 5. Applications |
Accueil > Éducation > Tutoriels
Notions fondamentales de télédétection
4.4 Traitement
Les opérations de pré-traitement, parfois appelées restauration et rectification d'image, sont conçues pour corriger les distorsions géométriques et radiométriques des plates-formes et capteurs spécifiques. Les corrections radiométriques peuvent être nécessaires à cause des variations dans l'illumination et dans la géométrie de visée d'une scène, des conditions atmosphériques, du bruit et de la réponse du capteur. Chacun de ces facteurs variera selon le capteur et la plate-forme utilisés, et selon les conditions d'acquisition des données. Aussi, il peut être souhaitable de convertir et de calibrer les données avec une unité de rayonnement ou réflexion connue (absolue) pour faciliter la comparaison entre les données.

Des variations dans la géométrie d'illumination et de visée entre les images (pour les capteurs optiques) peuvent être corrigées par la modélisation de la relation géométrique et la distance entre les aires de la surface terrestre observées, le Soleil et le capteur. Ceci est souvent requis pour pouvoir faire des comparaisons plus rapides entre des images prises par différents capteurs à différentes dates ou heures, ou pour faire des mosaïques d'images avec un seul capteur en maintenant les conditions d'illumination uniformes d'une scène à l'autre.
Comme nous l'avons vu au chapitre 1, la diffusion du rayonnement se produit quand il passe à travers l'atmosphère et qu'il interagit avec celle-ci. Cette diffusion peut réduire ou atténuer une partie de l'énergie illuminant la Terre. De plus, l'atmosphère atténuera aussi le signal se propageant de la cible au capteur.
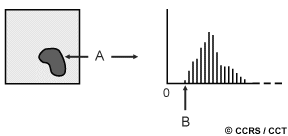
Diverses méthodes de corrections atmosphériques peuvent être appliquées, allant de modèles très détaillés des conditions atmosphériques durant l'acquisition des données, jusqu'à un simple calcul basé seulement sur les données de l'image. Un exemple de cette dernière méthode consiste à examiner l'intensité observée (valeur numérique du pixel) dans une région ombragée ou un objet très sombre (tel un grand lac clair -A) et à déterminer la valeur minimale (B) pour chacune des bandes spectrales. La correction est appliquée en soustrayant la valeur minimale observée, de tous les pixels dans chaque bande. Puisque la diffusion dépend de la longueur d'onde (chapitre 1), la valeur minimale variera d'une bande à l'autre. Cette méthode est basée sur la supposition que la réflexion de ces éléments est très petite, voire nulle si l'atmosphère est claire. Les valeurs plus petites que zéro que l'on pourrait observer sont dues à la diffusion atmosphérique.
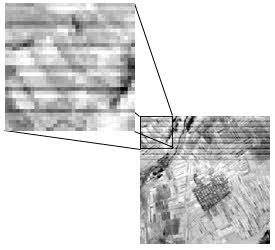 Le bruit dans une image peut être causé par des irrégularités ou des erreurs dans la réponse du capteur, ou par la transmission et l'enregistrement des données. Les formes les plus communes de bruits sont les rayures, le rubanement systématique et les lignes manquantes (B). Ces deux effets devraient être corrigés avant qu'un rehaussement ou une classification ne soient appliqués. Les rayures étaient fréquentes dans les premières données Landsat, à l'époque des six détecteurs MSS, à cause de la variation et de la dérive (voir texte anglais) dans la réponse.
Le bruit dans une image peut être causé par des irrégularités ou des erreurs dans la réponse du capteur, ou par la transmission et l'enregistrement des données. Les formes les plus communes de bruits sont les rayures, le rubanement systématique et les lignes manquantes (B). Ces deux effets devraient être corrigés avant qu'un rehaussement ou une classification ne soient appliqués. Les rayures étaient fréquentes dans les premières données Landsat, à l'époque des six détecteurs MSS, à cause de la variation et de la dérive (voir texte anglais) dans la réponse.  La dérive était différente pour chacun des six détecteurs, ce qui causait une représentation différente de la même intensité pour chaque détecteur et produisait sur l'image un effet de rayure. Le processus de correction faisait une correction relative de chacun des six capteurs pour amener leurs valeurs apparentes au même niveau. Les lignes manquantes apparaissent quand il y a des erreurs de systèmes qui résultent en l'absence de données ou en données déficientes le long d'une ligne de balayage. Les lignes manquantes sont habituellement 'corrigées' en remplaçant chaque ligne avec la valeur des pixels de la ligne au-dessus ou au-dessous, ou avec la moyenne des deux.
La dérive était différente pour chacun des six détecteurs, ce qui causait une représentation différente de la même intensité pour chaque détecteur et produisait sur l'image un effet de rayure. Le processus de correction faisait une correction relative de chacun des six capteurs pour amener leurs valeurs apparentes au même niveau. Les lignes manquantes apparaissent quand il y a des erreurs de systèmes qui résultent en l'absence de données ou en données déficientes le long d'une ligne de balayage. Les lignes manquantes sont habituellement 'corrigées' en remplaçant chaque ligne avec la valeur des pixels de la ligne au-dessus ou au-dessous, ou avec la moyenne des deux.
Pour plusieurs applications quantitatives de données de télédétection, il est nécessaire de convertir les nombres en unités représentant la réflectance ou l'émission actuelle de la surface. Ceci se fait en se basant sur les connaissances détaillées de la réponse du capteur et de la manière dont le signal analogique (c.-à-d. le rayonnement réfléchi ou émis) est converti en un nombre numérique, appelé conversion analogique-à-numérique. En inversant cette opération, le rayonnement absolu peut être calculé pour chaque pixel, de sorte qu'avec le temps, l'on peut effectuer une comparaison précise entre différents capteurs.
À la section 2.10, nous avons vu que toute les imageries de télédétection sont sujettes à des distorsions géométriques. Ces distorsions peuvent être dues à différents facteurs, notamment la perspective des capteurs optiques, le mouvement du système de balayage, le mouvement de la plate-forme, l'altitude, l'orientation et la vitesse de la plate-forme, le relief du terrain, la courbure et la rotation de la Terre. Les corrections géométriques sont appliquées pour compenser ces distorsions afin que la représentation géométrique de l'imagerie soit aussi proche que possible de la réalité. Plusieurs de ces variations sont systématiques ou prévisibles, et on peut en tenir compte par une modélisation précise du mouvement de la plate-forme et du capteur, et par la relation géométrique entre la plate-forme et la Terre. D'autres erreurs non systématiques, ou aléatoires, ne peuvent pas être modélisées de cette manière et on doit effectuer la correspondance géométrique de l'imagerie à un système connu de coordonnées au sol.
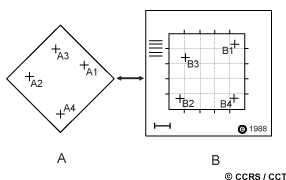
Le processus de correction géométrique consiste à identifier des coordonnées de l'image (c'est-à-dire ligne et colonne) de plusieurs points clairement distincts, appelés points de contrôle au sol (PCS), sur l'image à corriger (A -A1 à A4) et à les assortir à leur véritable position en coordonnées au sol (par exemple en latitude et longitude). Les vraies coordonnées au sol sont habituellement mesurées à partir d'une carte (B - B1 à B4), soit sur papier ou en format numérique. Ceci est une correction de type "image-à-carte". Une fois que plusieurs couples de PCS bien distribuées ont été identifiés, l'information est traitée par l'ordinateur pour déterminer les équations de transformation à être appliquées aux coordonnées originales (ligne et colonne) pour obtenir les nouvelles coordonnées au sol. La correction géométrique peut aussi être effectuée d'une image à une autre image plutôt qu'à des coordonnées géographiques. Cette méthode s'appelle correction enregistrement image-à-image, et on l'utilise souvent avant d'effectuer les différents procédés de transformation qui seront présentés dans la section 4.6.
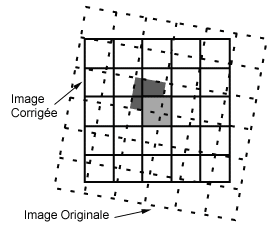
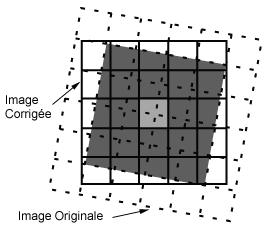
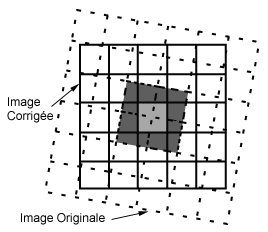 Pour effectuer une correction géométrique de l'image originale, on applique un procédé appelé rééchantillonnage afin de déterminer la valeur numérique à placer dans la nouvelle localisation du pixel de l'image de sortie corrigée. Le processus de rééchantillonnage calcule la nouvelle valeur du pixel à partir de sa valeur originale dans l'image non corrigée. Il existe trois principales méthodes de rééchantillonnage : le plus proche voisin, l'interpolation bilinéaire et la convolution cubique. La méthode du plus proche voisin utilise la valeur numérique du pixel de l'image originale qui se trouve le plus près de la localisation du nouveau pixel dans l'image corrigée. C'est la méthode la plus simple et elle n'altère pas la valeur originale, mais elle peut produire une duplication des pixels ou une perte de certaines valeurs. Cette méthode a aussi tendance à produire des images bruitées. L'interpolation bilinéaire prend une moyenne pondérée par la distance des quatre pixels de l'image originale les plus près du nouveau pixel. Le procédé de moyenne altère la valeur originale des pixels et crée une valeur complètement nouvelle sur l'image finale. Ceci peut être nuisible si d'autres procédés, tels que la classification basée sur la réponse spectrale, doivent être faits. Dans ce cas, il peut être préférable d'appliquer le rééchantillonnage après le processus de classification. Le processus de convolution cubique va encore plus loin et calcule la moyenne pondérée par la distance sur un bloc de seize pixels à partir de l'image originale entourant la localisation du nouveau pixel de sortie. Comme pour l'interpolation bilinéaire, cette méthode résulte en de nouvelles valeurs de pixels. Cependant, ces deux méthodes produisent des images à l'apparence plus douce, contrairement à la méthode du plus proche voisin.
Pour effectuer une correction géométrique de l'image originale, on applique un procédé appelé rééchantillonnage afin de déterminer la valeur numérique à placer dans la nouvelle localisation du pixel de l'image de sortie corrigée. Le processus de rééchantillonnage calcule la nouvelle valeur du pixel à partir de sa valeur originale dans l'image non corrigée. Il existe trois principales méthodes de rééchantillonnage : le plus proche voisin, l'interpolation bilinéaire et la convolution cubique. La méthode du plus proche voisin utilise la valeur numérique du pixel de l'image originale qui se trouve le plus près de la localisation du nouveau pixel dans l'image corrigée. C'est la méthode la plus simple et elle n'altère pas la valeur originale, mais elle peut produire une duplication des pixels ou une perte de certaines valeurs. Cette méthode a aussi tendance à produire des images bruitées. L'interpolation bilinéaire prend une moyenne pondérée par la distance des quatre pixels de l'image originale les plus près du nouveau pixel. Le procédé de moyenne altère la valeur originale des pixels et crée une valeur complètement nouvelle sur l'image finale. Ceci peut être nuisible si d'autres procédés, tels que la classification basée sur la réponse spectrale, doivent être faits. Dans ce cas, il peut être préférable d'appliquer le rééchantillonnage après le processus de classification. Le processus de convolution cubique va encore plus loin et calcule la moyenne pondérée par la distance sur un bloc de seize pixels à partir de l'image originale entourant la localisation du nouveau pixel de sortie. Comme pour l'interpolation bilinéaire, cette méthode résulte en de nouvelles valeurs de pixels. Cependant, ces deux méthodes produisent des images à l'apparence plus douce, contrairement à la méthode du plus proche voisin.
| Mise à jour : 2002-08-21 | Avis importants |
