
| Table of Contents |
| 1. Introduction 2. Sensors 3. Microwaves |
4. Image Analysis |
| 5. Applications |
Fundamentals of Remote Sensing
4.4 Pre-processing
Pre-processing operations, sometimes referred to as image restoration and rectification, are intended to correct for sensor- and platform-specific radiometric and geometric distortions of data. Radiometric corrections may be necessary due to variations in scene illumination and viewing geometry, atmospheric conditions, and sensor noise and response. Each of these will vary depending on the specific sensor and platform used to acquire the data and the conditions during data acquisition. Also, it may be desirable to convert and/or calibrate the data to known (absolute) radiation or reflectance units to facilitate comparison between data.

Variations in illumination and viewing geometry between images (for optical sensors) can be corrected by modeling the geometric relationship and distance between the area of the Earth's surface imaged, the sun, and the sensor. This is often required so as to be able to more readily compare images collected by different sensors at different dates or times, or to mosaic multiple images from a single sensor while maintaining uniform illumination conditions from scene to scene.
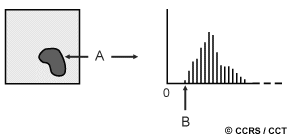
As we learned in Chapter 1, scattering of radiation occurs as it passes through and interacts with the atmosphere. This scattering may reduce, or attenuate, some of the energy illuminating the surface. In addition, the atmosphere will further attenuate the signal propagating from the target to the sensor. Various methods of atmospheric correction can be applied ranging from detailed modeling of the atmospheric conditions during data acquisition, to simple calculations based solely on the image data. An example of the latter method is to examine the observed brightness values (digital numbers), in an area of shadow or for a very dark object (such as a large clear lake - A) and determine the minimum value (B). The correction is applied by subtracting the minimum observed value, determined for each specific band, from all pixel values in each respective band. Since scattering is wavelength dependent (Chapter 1), the minimum values will vary from band to band. This method is based on the assumption that the reflectance from these features, if the atmosphere is clear, should be very small, if not zero. If we observe values much greater than zero, then they are considered to have resulted from atmospheric scattering.
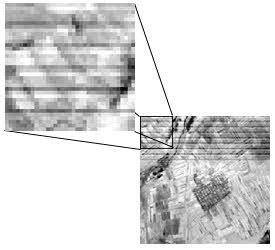 Noise in an image may be due to irregularities or errors that occur in the sensor response and/or data recording and transmission. Common forms of noise include systematic striping or banding and dropped lines. Both of these effects should be corrected before further enhancement or classification is performed. Striping was common in early Landsat MSS data due to variations and drift in the response over time of the six MSS detectors.
Noise in an image may be due to irregularities or errors that occur in the sensor response and/or data recording and transmission. Common forms of noise include systematic striping or banding and dropped lines. Both of these effects should be corrected before further enhancement or classification is performed. Striping was common in early Landsat MSS data due to variations and drift in the response over time of the six MSS detectors.  The "drift" was different for each of the six detectors, causing the same brightness to be represented differently by each detector. The overall appearance was thus a 'striped' effect. The corrective process made a relative correction among the six sensors to bring their apparent values in line with each other. Dropped lines occur when there are systems errors which result in missing or defective data along a scan line. Dropped lines are normally 'corrected' by replacing the line with the pixel values in the line above or below, or with the average of the two.
The "drift" was different for each of the six detectors, causing the same brightness to be represented differently by each detector. The overall appearance was thus a 'striped' effect. The corrective process made a relative correction among the six sensors to bring their apparent values in line with each other. Dropped lines occur when there are systems errors which result in missing or defective data along a scan line. Dropped lines are normally 'corrected' by replacing the line with the pixel values in the line above or below, or with the average of the two.
For many quantitative applications of remote sensing data, it is necessary to convert the digital numbers to measurements in units which represent the actual reflectance or emittance from the surface. This is done based on detailed knowledge of the sensor response and the way in which the analog signal (i.e. the reflected or emitted radiation) is converted to a digital number, called analog-to-digital (A-to-D) conversion. By solving this relationship in the reverse direction, the absolute radiance can be calculated for each pixel, so that comparisons can be accurately made over time and between different sensors.
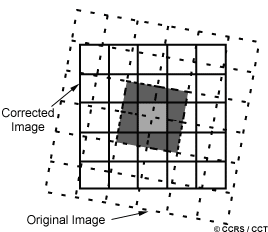
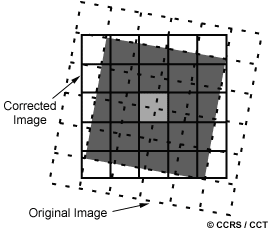
In section 2.10 in Chapter 2, we learned that all remote sensing imagery are inherently subject to geometric distortions. These distortions may be due to several factors, including: the perspective of the sensor optics; the motion of the scanning system; the motion of the platform; the platform altitude, attitude, and velocity; the terrain relief; and, the curvature and rotation of the Earth. Geometric corrections are intended to compensate for these distortions so that the geometric representation of the imagery will be as close as possible to the real world. Many of these variations are systematic, or predictable in nature and can be accounted for by accurate modeling of the sensor and platform motion and the geometric relationship of the platform with the Earth. Other unsystematic, or random, errors cannot be modeled and corrected in this way. Therefore, geometric registration of the imagery to a known ground coordinate system must be performed.
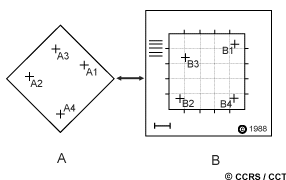
The geometric registration process involves identifying the image coordinates (i.e. row, column) of several clearly discernible points, called ground control points (or GCPs), in the distorted image (A - A1 to A4), and matching them to their true positions in ground coordinates (e.g. latitude, longitude). The true ground coordinates are typically measured from a map (B - B1 to B4), either in paper or digital format. This is image-to-map registration. Once several well-distributed GCP pairs have been identified, the coordinate information is processed by the computer to determine the proper transformation equations to apply to the original (row and column) image coordinates to map them into their new ground coordinates. Geometric registration may also be performed by registering one (or more) images to another image, instead of to geographic coordinates. This is called image-to-image registration and is often done prior to performing various image transformation procedures, which will be discussed in section 4.6, or for multitemporal image comparison.
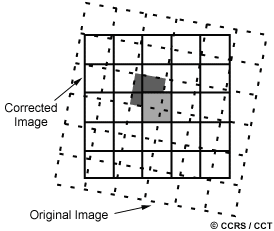
In order to actually geometrically correct the original distorted image, a procedure called resampling is used to determine the digital values to place in the new pixel locations of the corrected output image. The resampling process calculates the new pixel values from the original digital pixel values in the uncorrected image. There are three common methods for resampling: nearest neighbour, bilinear interpolation, and cubic convolution. Nearest neighbour resampling uses the digital value from the pixel in the original image which is nearest to the new pixel location in the corrected image. This is the simplest method and does not alter the original values, but may result in some pixel values being duplicated while others are lost. This method also tends to result in a disjointed or blocky image appearance.
 Bilinear interpolation resampling takes a weighted average of four pixels in the original image nearest to the new pixel location. The averaging process alters the original pixel values and creates entirely new digital values in the output image. This may be undesirable if further processing and analysis, such as classification based on spectral response, is to be done. If this is the case, resampling may best be done after the classification process. Cubic convolution resampling goes even further to calculate a distance weighted average of a block of sixteen pixels from the original image which surround the new output pixel location. As with bilinear interpolation, this method results in completely new pixel values. However, these two methods both produce images which have a much sharper appearance and avoid the blocky appearance of the nearest neighbour method.
Bilinear interpolation resampling takes a weighted average of four pixels in the original image nearest to the new pixel location. The averaging process alters the original pixel values and creates entirely new digital values in the output image. This may be undesirable if further processing and analysis, such as classification based on spectral response, is to be done. If this is the case, resampling may best be done after the classification process. Cubic convolution resampling goes even further to calculate a distance weighted average of a block of sixteen pixels from the original image which surround the new output pixel location. As with bilinear interpolation, this method results in completely new pixel values. However, these two methods both produce images which have a much sharper appearance and avoid the blocky appearance of the nearest neighbour method.
| Updated2002-08-21 | Important Notices |
